Advertisements
Advertisements
Question
In the given figure, if BP || CQ and AC = BC, then the measure of x is
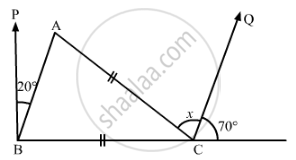
Options
20°
25°
30°
35°
Advertisements
Solution
In the given figure, BP || CQ and AC || BC
We need to find the measure of x
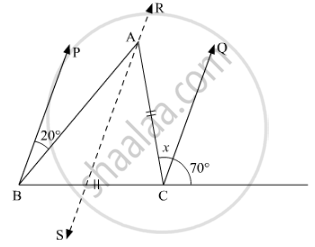
Here, we draw a line RS parallel to BP, i.e BP || RS
Also, using the property, “two lines parallel to the same line are parallel to each other”
As,
BP || RS
BP || CQ
Thus, RS || CQ
Now, BP || RS and BA is the transversal, so using the property, “alternate interior angles are equal”
∠PBA = ∠BAS
∠BAS = 20° .......... (1)
Similarly, CQ|| RS and AC is the transversal
∠QCA = ∠SAC
∠SAC = x ........(2)
Adding (1) and (2), we get
∠SAC + ∠BAS = 20° + x
∠A = 20° + x
Also, as AC = BC
Using the property,”angles opposite to equal sides are equal”, we get
∠ABC = ∠CAB
∠ABC = 20° + x
Further, using the property, “an exterior angle is equal to the sum of the two opposite interior angles”
In ΔABC
ext. ∠C = ∠CAB + ∠ABC
70° + x = 20° + x + 20° + x
70° + x = 40° + 2x
70° - 40° = 2x - x
x = 30°
Thus, x = 30°
APPEARS IN
RELATED QUESTIONS
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
Find the measure of each exterior angle of an equilateral triangle.
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
The angles of a right angled triangle are
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
