Advertisements
Advertisements
Question
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
Solution
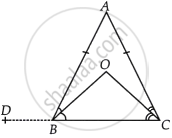
Given: ΔABC is an isosceles triangle in which AB = AC, BO and CO are the bisectors of ∠ABC and ∠ACB respectively intersect at O.
To show: ∠DBA = ∠BOC
Construction: Line CB produced to D.
Proof: In ΔABC, AB = AC ...[Given]
∠ACB = ∠ABC ...[Angles opposite to equal sides are equal]
⇒ `1/2 ∠ACB = 1/2 ∠ABC` ...[On dividing both sides by 2]
⇒ ∠OCB = ∠OBC ...(i) [∵ BO and CO are the bisectors of ∠ABC and ∠ACB]
In ΔBOC, ∠OBC + ∠OCB + ∠BOC = 180° ...[By angle sum property of a triangle]
⇒ ∠OBC + ∠OBC + ∠BOC = 180° ...[From equation (i)]
⇒ 2∠OBC + ∠BOC = 180°
⇒ ∠ABC + ∠BOC = 180° ...[∵ BO is the bisector of ∠ABC]
⇒ 180° – ∠DBA + ∠BOC = 180° ...[∵ DBC is a straight line]
⇒ – ∠DBA + ∠BOC = 0
⇒ ∠DBA = ∠BOC
APPEARS IN
RELATED QUESTIONS
Show that the angles of an equilateral triangle are 60° each.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Prove that the medians of an equilateral triangle are equal.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
