Advertisements
Advertisements
Question
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Solution
Given in the question, bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Now BO is produced to a point M.
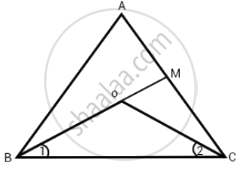
In triangle ABC,
AB = AC
∠ABC = ∠ACB ...[Angle opposite to equal sides of a triangle are equal]
`1/2 ∠ABC = 1/2 ∠ACB`
That is ∠1 = ∠2 ...[Since, BO and CO are bisectors of ∠B and ∠C]
In triangle OBC,
Exterior ∠MOC = ∠1 + ∠2 ...[Exterior angle of a triangle is equal to the sum of interior opposite angles]
Exterior ∠MOC = 2∠1 ...[∠1 = ∠2]
Hence, ∠MOC = ∠ABC.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if ∠A = 55°, ∠B = 40°, find ∠C.
Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
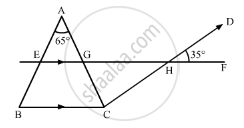
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
Find x, if the angles of a triangle is:
x°, 2x°, 2x°
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
9 cm, 6 cm, 16 cm
The number of triangles in figure is ______.