Advertisements
Advertisements
प्रश्न
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
उत्तर
Given in the question, bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Now BO is produced to a point M.
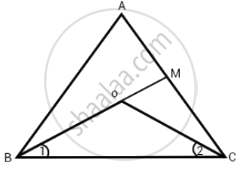
In triangle ABC,
AB = AC
∠ABC = ∠ACB ...[Angle opposite to equal sides of a triangle are equal]
`1/2 ∠ABC = 1/2 ∠ACB`
That is ∠1 = ∠2 ...[Since, BO and CO are bisectors of ∠B and ∠C]
In triangle OBC,
Exterior ∠MOC = ∠1 + ∠2 ...[Exterior angle of a triangle is equal to the sum of interior opposite angles]
Exterior ∠MOC = 2∠1 ...[∠1 = ∠2]
Hence, ∠MOC = ∠ABC.
APPEARS IN
संबंधित प्रश्न
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
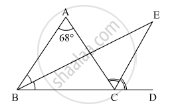
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Find the value of the angle in the given figure:
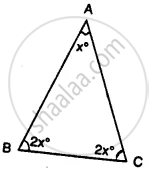
Find the unknown marked angles in the given figure:
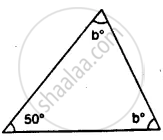
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
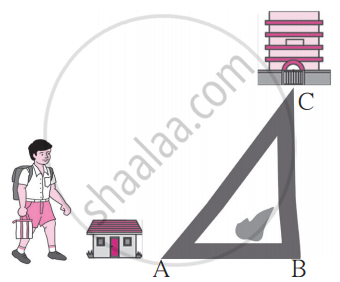
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
