Advertisements
Advertisements
प्रश्न
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
उत्तर
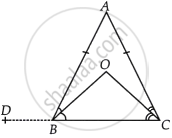
Given: ΔABC is an isosceles triangle in which AB = AC, BO and CO are the bisectors of ∠ABC and ∠ACB respectively intersect at O.
To show: ∠DBA = ∠BOC
Construction: Line CB produced to D.
Proof: In ΔABC, AB = AC ...[Given]
∠ACB = ∠ABC ...[Angles opposite to equal sides are equal]
⇒ `1/2 ∠ACB = 1/2 ∠ABC` ...[On dividing both sides by 2]
⇒ ∠OCB = ∠OBC ...(i) [∵ BO and CO are the bisectors of ∠ABC and ∠ACB]
In ΔBOC, ∠OBC + ∠OCB + ∠BOC = 180° ...[By angle sum property of a triangle]
⇒ ∠OBC + ∠OBC + ∠BOC = 180° ...[From equation (i)]
⇒ 2∠OBC + ∠BOC = 180°
⇒ ∠ABC + ∠BOC = 180° ...[∵ BO is the bisector of ∠ABC]
⇒ 180° – ∠DBA + ∠BOC = 180° ...[∵ DBC is a straight line]
⇒ – ∠DBA + ∠BOC = 0
⇒ ∠DBA = ∠BOC
APPEARS IN
संबंधित प्रश्न
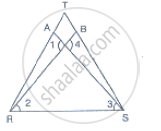
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Fill the blank in the following so that the following statement is true.
In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
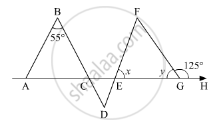
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
