Advertisements
Advertisements
प्रश्न
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
उत्तर
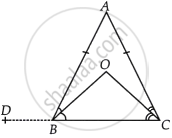
Given: ΔABC is an isosceles triangle in which AB = AC, BO and CO are the bisectors of ∠ABC and ∠ACB respectively intersect at O.
To show: ∠DBA = ∠BOC
Construction: Line CB produced to D.
Proof: In ΔABC, AB = AC ...[Given]
∠ACB = ∠ABC ...[Angles opposite to equal sides are equal]
⇒ `1/2 ∠ACB = 1/2 ∠ABC` ...[On dividing both sides by 2]
⇒ ∠OCB = ∠OBC ...(i) [∵ BO and CO are the bisectors of ∠ABC and ∠ACB]
In ΔBOC, ∠OBC + ∠OCB + ∠BOC = 180° ...[By angle sum property of a triangle]
⇒ ∠OBC + ∠OBC + ∠BOC = 180° ...[From equation (i)]
⇒ 2∠OBC + ∠BOC = 180°
⇒ ∠ABC + ∠BOC = 180° ...[∵ BO is the bisector of ∠ABC]
⇒ 180° – ∠DBA + ∠BOC = 180° ...[∵ DBC is a straight line]
⇒ – ∠DBA + ∠BOC = 0
⇒ ∠DBA = ∠BOC
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
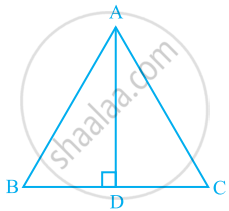
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
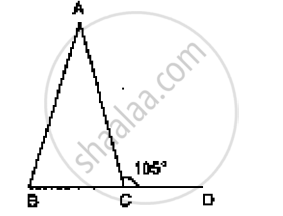
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
In the given figure, if AB ⊥ BC. then x =
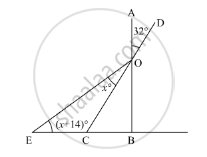
In the given figure, what is the value of x?
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
