Advertisements
Advertisements
प्रश्न
In the given figure, if AB ⊥ BC. then x =
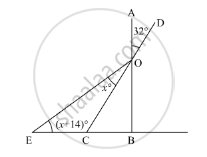
विकल्प
18
22
25
32
Advertisements
उत्तर
In the given figure, AB ⊥ BC
We need to find the value of x.
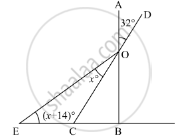
Now, since AB and CD are straight lines intersecting at point O, using the property, “vertically opposite angles are equal”, we get,
∠BOC = ∠AOD
∠BOC = 32°
Further, applying angle sum property of the triangle
In ΔBOC
∠BOC + ∠OBC + ∠BCO = 180°
32° + 90° + ∠BCO = 180°
∠BCO = 180° -122°
∠BCO = 58°
Then, using the property, “an exterior angle of the triangle is equal to the sum of the two opposite interior angles”, we get,
In ΔEOC
∠BCO = ∠OEC +∠EOC
58° = (x + 14)° + x
58° = 2x + 14°
2x = 58° - 14°
Further solving for x, we get,
2x = 44°
`x = (44° )/2`
x = 22°
Thus x = 22°
APPEARS IN
संबंधित प्रश्न
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
If altitudes CE and BF of a triangle ABC are equal, then AB = ....
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
In the given figure, if l1 || l2, the value of x is
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
