Advertisements
Advertisements
प्रश्न
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
विकल्प
3.6 cm
4.1 cm
3.8 cm
3.4 cm
उत्तर
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be 3.4 cm.
Explanation:
Given, the length of two sides of a triangle are 5 cm and 1.5 cm, respectively.
Let sides AB = 5 cm and CA = 1.5 cm
We know that, a closed figure formed by three intersecting lines (or sides) is called a triangle, if difference of two sides < third side and sum of two sides > third side
∴ 5 – 1.5 < BC and 5 + 1.5 > BC
⇒ 3.5 < BC and 6.5 > BC
Here, we see that options (a), (b) and (c) satisfy the above inequality but option (d) does not satisfy the above inequality.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

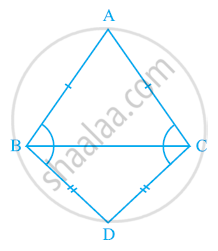
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
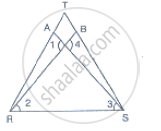
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
Fill the blank in the following so that the following statement is true.
In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
Fill in the blank to make the following statement true.
The sum of any two sides of a triangle is .... than the third side.
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
