Advertisements
Advertisements
प्रश्न
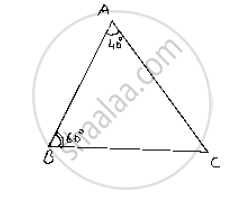
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
उत्तर
Given that in , ΔABC ∠A =40° and ∠B=60° We have to find longest and shortest side We know that,
Sum of angles in a triangle180°
⇒∠A+∠B+∠C=180°
⇒40°+60°+∠C=180°
⇒∠C=180° -(40° +60° )
=180° -100° =80°
∴∠C = 80°
Now,
⇒ 40<60<80⇒∠A< ∠B < ∠C
⇒ ∠Cis greater angle and ∠A is smaller angle
Now, ∠A<∠B<∠C
⇒ BC<AAC<AB
[∵Side opposite to greater angle is larger and side opposite to smaller angle is smaller]
∴ AB is longest and BC is smallest or shortest side.
APPEARS IN
संबंधित प्रश्न
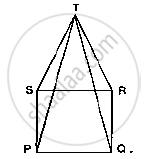
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F):
The measure of each angle of an equilateral triangle is 60°
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
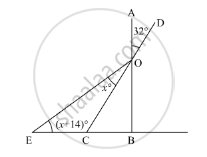
In the given figure, if AB ⊥ BC. then x =
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
