Advertisements
Advertisements
प्रश्न
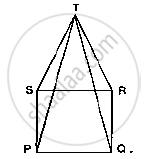
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
Advertisements
उत्तर
Given that PQRS is a square and SRT is an equilateral triangle. And given to prove that
PT = QT and ∠ TQR =15 °
Now , PQRS is a square
⇒ PQ =QR=RS=SP ....................... (1)
And also, SRT is an equilateral triangle.
⇒ SR = RT=TS .............................(2)
And ∠TSR = ∠SRT= ∠RTS = 60°
From (1) and (2)
PQ=QR=SP=SR=RT=TS ...........................(3)
And also,
∠TSR=∠TSR+∠RSP= 60° +90° +150°
∠TRQ=∠TRS+∠SRQ=60°+90°+150°
⇒ ∠TSR=∠TRQ=150° ............................(4)
Now, in Δ TSR and Δ TRQ
TS=TR [from (3)]Δ
∠TSP = ∠TRQ [from (4)]
SP=RQ [from (3)]
So, by SAS ccongruence criterion we have
Δ TSR ≅ Δ TRQ
⇒ PT=QT [corresponding parts of congruent triangles are equal ]
Consider Δ TQR,
QR= TR [from (3)]
⇒ Δ TQR is a isosceles triangle
∠QTR=∠TQR [angles opposite to equal sides]
Now,
Sum of angles in a traingle is qual to 180°
⇒ ∠ QTR+∠TQR + ∠TRQ =180°
⇒ 2∠TQR+150°=180 [from (4)]
⇒ 2∠TQR = 180° -150°
⇒ 2 ∠TQR = 30° ∠TQR=15 °
∴ Hence Proved
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
Show that the angles of an equilateral triangle are 60° each.
Find the measure of each exterior angle of an equilateral triangle.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
If the measures of angles of a triangle are in the ratio of 3 : 4 : 5, what is the measure of the smallest angle of the triangle?
In the given figure, for which value of x is l1 || l2?
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
