Advertisements
Advertisements
प्रश्न
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
Advertisements
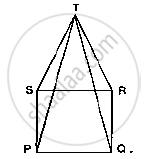
उत्तर
Given that PQRS is a square and SRT is an equilateral triangle. And given to prove that
PT = QT and ∠ TQR =15 °
Now , PQRS is a square
⇒ PQ =QR=RS=SP ....................... (1)
And also, SRT is an equilateral triangle.
⇒ SR = RT=TS .............................(2)
And ∠TSR = ∠SRT= ∠RTS = 60°
From (1) and (2)
PQ=QR=SP=SR=RT=TS ...........................(3)
And also,
∠TSR=∠TSR+∠RSP= 60° +90° +150°
∠TRQ=∠TRS+∠SRQ=60°+90°+150°
⇒ ∠TSR=∠TRQ=150° ............................(4)
Now, in Δ TSR and Δ TRQ
TS=TR [from (3)]Δ
∠TSP = ∠TRQ [from (4)]
SP=RQ [from (3)]
So, by SAS ccongruence criterion we have
Δ TSR ≅ Δ TRQ
⇒ PT=QT [corresponding parts of congruent triangles are equal ]
Consider Δ TQR,
QR= TR [from (3)]
⇒ Δ TQR is a isosceles triangle
∠QTR=∠TQR [angles opposite to equal sides]
Now,
Sum of angles in a traingle is qual to 180°
⇒ ∠ QTR+∠TQR + ∠TRQ =180°
⇒ 2∠TQR+150°=180 [from (4)]
⇒ 2∠TQR = 180° -150°
⇒ 2 ∠TQR = 30° ∠TQR=15 °
∴ Hence Proved
APPEARS IN
संबंधित प्रश्न
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
Prove that the medians of an equilateral triangle are equal.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
In the given figure, the value of x is ______.
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then
Which of the following correctly describes the given triangle?
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
