Advertisements
Advertisements
प्रश्न
Prove that the medians of an equilateral triangle are equal.
उत्तर
Given to prove that the medians of an equilateral triangle are equal
Median: The line joining the vertex and midpoint of opposite side.
Now, consider an equilateral triangle ABC
Let D,E,F are midpoints of , BC CAand . AB
Then, , AD BE and CF are medians of . Δ ABC
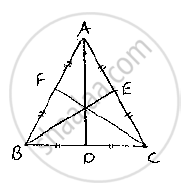
Now ,
D is midpoint of BC⇒ BD = DC =`(BC)/2`
Similarly ,` CE=EA=(AC)/2`
`AF= FB=(AB)/2`
Since Δ ABC is an equilateral traingle ⇒ AB=BC= CA .............(1)
`BD=DC=CE=EA=AF=FB= (BC)/2=(AC)/2 (AB)/2` ..............(2)
And also , ∠ ABC= ∠ BCA=∠CAB=60° ..................(3)
Now, consider Δ ABD and Δ BCE
AB=BC [from (1)]
BD= CE [from (2)]
∠ ABD= ∠ BCE [from (3)] [∠ ABD and ∠ ABC and ∠ BCE and BCA aare same ]
So, from SAS congruence criterion , we have
Δ ABD ≅ Δ BCE
AD= BE ........................(4)
[corresponding parts of congruent triangles are equal]
Now, consider ΔBCE and Δ CAF,
BC = CA [from (1)]
∠BCE =∠ CAF [from (3)]
[∠ BCE and ∠ BCA and ∠ CAF annd ∠ CAB are same ]
CE=AF [from (2)]
So, from SAS congruence criterion, we have Δ BCE≅ Δ CAF
⇒ BE=CF ..........................(5)
[Corresponding parts of congruent triangles are equal ]
From (4) and (5), we have
AD =BE= CF
⇒Median AD = Median BE = Median CF
∴The medians of an equilateral triangle are equal
∴Hence proved
APPEARS IN
संबंधित प्रश्न
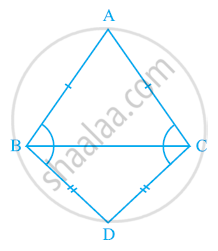
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
Fill the blank in the following so that the following statement is true.
Angle opposite to equal sides of a triangle are .....
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
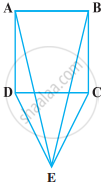
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
