Advertisements
Advertisements
प्रश्न
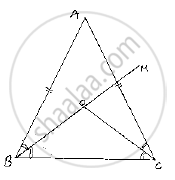
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
उत्तर
Given that in , ΔABC,
AB=AC and the bisector of ∠B and ∠C intersect at O and M is
a point on BO produced
We have to prove ∠ MOC=∠ABC
Since,
AB =AC ⇒ΔABC is isosceles ⇒ ∠B=∠C(or) ∠ABC=∠ACB
Now,
BO and CO are bisectors of ∠ABC and ∠ACB respectively
⇒ABO=∠OBC=∠ACO=∠OB=`1/2` ∠ABC=`1/2`∠ACB ............(1)
We have, in ΔOBC
∠OBC +∠OCB +∠BOC =180° .............(2)
And also
∠BOC +∠COM =180° ..................(3)[Straight angle]
Equating (2) and (3)
⇒ ∠OBC+∠OCB+-∠BOC=∠BOC+∠MOC
⇒ ∠OBC+∠OBC=∠MOC [∵ from (1)]
⇒ 2∠OBBC=∠MOC
⇒2`(1/2∠ABC)`=∠MOC [∵from (1)]
⇒ ∠ABC=∠MOC
∴ ∠MOC=∠ABC
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
The vertical angle of an isosceles triangle is 100°. Find its base angles.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
Angle opposite to equal sides of a triangle are .....
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
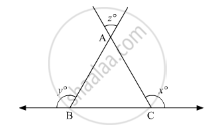
In the given figure, what is z in terms of x and y?
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
