Advertisements
Advertisements
प्रश्न
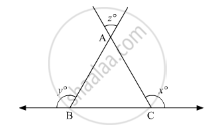
In the given figure, what is z in terms of x and y?
पर्याय
x + y + 180
x + y − 180
180° − (x + y)
x + y + 360°
उत्तर
In the given ΔABC, we need to convert z in terms of x and y
Now, BC is a straight line, so using the property, “angles forming a linear pair are supplementary”
∠ABC + y = 180
∠ABC =180° - y°
Similarly,
∠ACB + x° = 180°
∠ACB = 180° - x
Also, using the property, “vertically opposite angles are equal”, we get,
z = ∠BAC
Further, using angle sum property of the triangle
∠BAC + ∠ABC + ∠ACB = 180°
z° + (180°- y°) + (180° - x°) = 180°
360° + z° - y° - x° = 180°
180° + z° = y° + x°
z° = y°+ x° -180°
Thus, z = y + x -180°
APPEARS IN
संबंधित प्रश्न
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
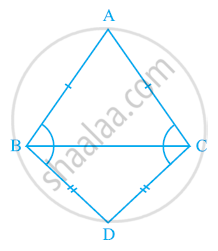
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
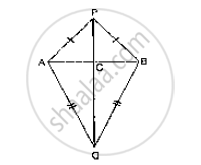
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Prove that each angle of an equilateral triangle is 60°.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
The angles of a right angled triangle are
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
