Advertisements
Advertisements
प्रश्न
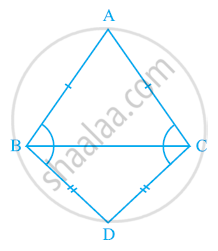
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
उत्तर
In isosceles △ABC,
AB = AC ...[ABC is an isosceles triangle]
∴ ∠ACB = ∠ABC …(i) ...[Angles opposite to equal sides of a triangle are equal]
Also, in isosceles △BCD,
BD = DC ...[BDC is an isosceles triangle]
∴ ∠BCD = ∠CBD ...(ii) ...[Angles opposite to equal sides of a triangle are equal]
On adding the corresponding sides of (i) and (ii)
∠ACB + ∠BCD = ∠ABC + ∠CBD
⇒ ∠ACD = ∠ABD or ∠ABD = ∠ACD ...(By Corresponding parts of congruent triangles)
APPEARS IN
संबंधित प्रश्न
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
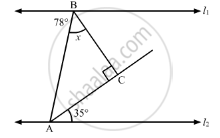
In the given figure, for which value of x is l1 || l2?
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
Find all the angles of an equilateral triangle.
