Advertisements
Advertisements
प्रश्न
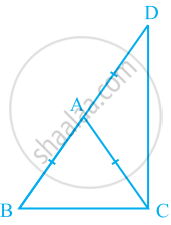
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
Advertisements
उत्तर
AB = AC ...[Given] ...(1)
AB = AD ...[Given] ...(2)
From (1) and (2), we have
AC = AD
Now, in ΔABC, we have
∠ABC + ∠ACB + ∠BAC = 180° ...[Angle sum property of a Δ]
⇒ 2∠ACB + ∠BAC = 180° ...(3) ...[∠ABC = ∠ACB (Angles opposite to equal sides of a Δ are equal)]
Similarly, in ΔACD,
∠ADC + ∠ACD + ∠CAD = 180°
⇒ 2∠ACD + ∠CAD = 180° ...(4) ...[∠ADC = ∠ACD (Angles opposite to equal sides of a Δ are equal)]
Adding (3) and (4), we have
2∠ACB + ∠BAC + 2∠ACD + ∠CAD = 180° +180°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2∠BCD + 180° = 360° ...[∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360° − 180°
⇒ 2∠BCD = 180°
⇒ ∠BCD = `(180°)/2`
Thus, ∠BCD = 90°
APPEARS IN
संबंधित प्रश्न
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
Find the measure of each exterior angle of an equilateral triangle.
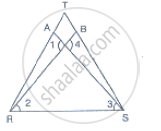
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Which of the following statements are true (T) and which are false (F):
The measure of each angle of an equilateral triangle is 60°
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
In Fig. 10.131, prove that: (i) CD + DA + AB + BC > 2AC (ii) CD + DA + AB > BC
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
Write the sum of the angles of an obtuse triangle.
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
In the given figure, if AB ⊥ BC. then x =
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
