Advertisements
Advertisements
प्रश्न
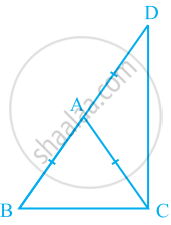
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
उत्तर
AB = AC ...[Given] ...(1)
AB = AD ...[Given] ...(2)
From (1) and (2), we have
AC = AD
Now, in ΔABC, we have
∠ABC + ∠ACB + ∠BAC = 180° ...[Angle sum property of a Δ]
⇒ 2∠ACB + ∠BAC = 180° ...(3) ...[∠ABC = ∠ACB (Angles opposite to equal sides of a Δ are equal)]
Similarly, in ΔACD,
∠ADC + ∠ACD + ∠CAD = 180°
⇒ 2∠ACD + ∠CAD = 180° ...(4) ...[∠ADC = ∠ACD (Angles opposite to equal sides of a Δ are equal)]
Adding (3) and (4), we have
2∠ACB + ∠BAC + 2∠ACD + ∠CAD = 180° +180°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2∠BCD + 180° = 360° ...[∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360° − 180°
⇒ 2∠BCD = 180°
⇒ ∠BCD = `(180°)/2`
Thus, ∠BCD = 90°
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
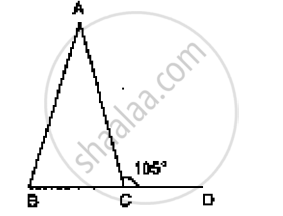
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
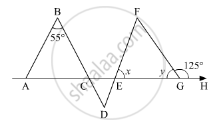
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
