Advertisements
Advertisements
प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
उत्तर

(i) ABC is an isosceles triangle in which AB = AC
∠C = ∠B ...[Angles opposite to equal sides in a triangle are equal.]
⇒ ∠OCA + ∠OCB = ∠OBA + ∠OBC
⇒ ∠OCB + ∠OCB = ∠OBC + ∠OBC
∵ OB bisects ∠B.
∴ ∠OBA = ∠OBC
And OC bisects ∠C.
∴ ∠OCA = ∠OCB
⇒ 2∠OCB = 2∠OBC
⇒ ∠OCB = ∠OBC
Now, in △OBC,
∠OCB = ∠OBC ...[Proved above]
∴ OB = OC ...[Sides opposite to equal angles]
(ii) Now, in △AOB and △AOC,
AB = AC ...[Given]
∠OBA = ∠OCA
∠B = ∠C
BO bisects ∠B and CO bisects ∠C.
∠OBA = ∠OCA
OB = OC
∴ △AOB ≌ △AOC ...[By SAS congruence rule]
⇒ ∠OAB = ∠OAC ...[Corresponding parts of congruent triangles]
So, AO bisects ∠A.
APPEARS IN
संबंधित प्रश्न
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that LN = MN.
Fill the blank in the following so that the following statement is true.
If altitudes CE and BF of a triangle ABC are equal, then AB = ....
Fill the blank in the following so that the following statement is true.
In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
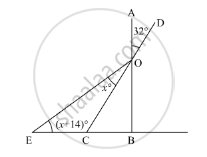
In the given figure, if AB ⊥ BC. then x =
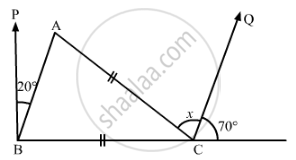
In the given figure, if BP || CQ and AC = BC, then the measure of x is
Which of the following correctly describes the given triangle?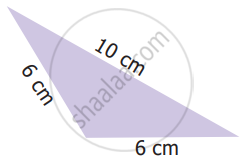
In ∆PQR, if ∠R > ∠Q, then ______.
