Advertisements
Advertisements
प्रश्न
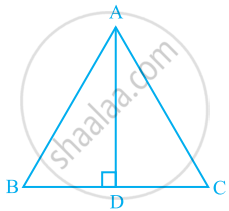
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
उत्तर
Since AD is the bisector of BC.
∴ BD = CD
Now, in △ABD and △ACD, we have
AD = DA ...[Common]
∠ADB = ∠ADC ...[Each 90°]
BD = CD ...[Proved above]
∴ △ABD ≌ △ACD ...[By SAS congruence]
⇒ AB = AC ...[By Corresponding parts of congruent triangles]
Thus, △ABC is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
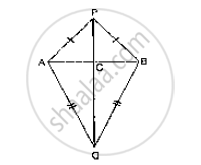
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
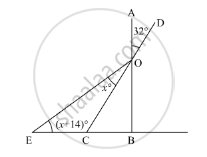
In the given figure, if AB ⊥ BC. then x =
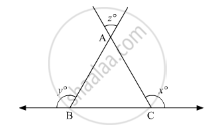
In the given figure, what is z in terms of x and y?
The angles of a right angled triangle are
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
