Advertisements
Advertisements
प्रश्न
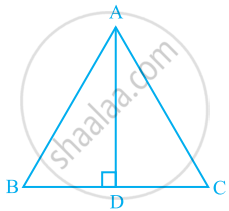
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
उत्तर
Since AD is the bisector of BC.
∴ BD = CD
Now, in △ABD and △ACD, we have
AD = DA ...[Common]
∠ADB = ∠ADC ...[Each 90°]
BD = CD ...[Proved above]
∴ △ABD ≌ △ACD ...[By SAS congruence]
⇒ AB = AC ...[By Corresponding parts of congruent triangles]
Thus, △ABC is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
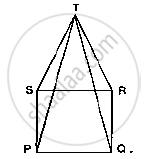
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
