Advertisements
Advertisements
प्रश्न
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
उत्तर
Given that O is any point in the interior of ABC
We have to prove
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >`1/2`(AB + BC + CA)
We know that, in a triangle the sum of any two sides is greater than the third side So, we have
In ΔABC
AB+BC>AC
BC+AC>AB
AC+AB>BC
In ΔOBC
OB+OC>BC ...........(1)
In ΔOAC
OA+OC>AC ...........(2)
In ΔOAB
OA+OB>AB ............(3)
Now, extend (or) produce BO to meet AC in D.
Now, in ΔABD,we have
AB+AD+BD
⇒ AB+AD>BO+OD .............(4) [∵ BD=BO+OD]
Similarly in , ΔODC we have
OD+DC>OC ...............(5)
(1) Adding (4) and (5), we get
AB+AD+OD+DC>BO+OD+OC
⇒AB+(AD+DC)>OB+OC
⇒ AB+AC>OB+OC ...............(6)
Similarly, we have
BC+BA>OA+OC ...............(7)
and CA+CB>OA+OB ..............(8)
(2) Adding equation (6), (7) and (8), we get
AB+AC+BC+BA+CA+CB>OB+OC+OA+OC+OA+OB
⇒2AB+2BC+CA>2OA+2OB+2OC
⇒2(AB+BC+CA>OA+OB+OC)
⇒AB+BC+CA>OA+OB+OC
(3) Adding equations (1), (2) and (3)
OB+OC+OA+OC+OA+OB+>BC+AC+AB
⇒2OA+2OB+2OC>AB+BC+CA
We get⇒ 2(OA+OB+OC)>AB+BC+CA
∴ (OA+OB+OC)>`1/2`(AB+BC+CA)
APPEARS IN
संबंधित प्रश्न
Find the measure of each exterior angle of an equilateral triangle.
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
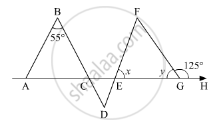
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
