Advertisements
Advertisements
प्रश्न
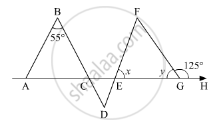
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
उत्तर
In the given figure,,,and AB ||DE ,BD || FG , ∠FGH =125° and ∠B = 55°
We need to find the value of x and y
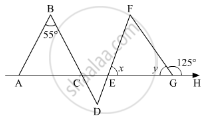
Here, as AB || DE and BD is the transversal, so according to the property, “alternate interior angles are equal”, we get
∠D = ∠B
∠D = 55° ............. (1)
Similarly, as BD || FG and DF is the transversal
∠D = ∠F
∠F = 55° (Using 1)
Further, EGH is a straight line. So, using the property, angles forming a linear pair are supplementary
∠FGE + ∠FGH = 180°
y + 125° = 180°
y = 180° - 125°
y = 55°
Also, using the property, “an exterior angle of a triangle is equal to the sum of the two opposite interior angles”, we get,
In ΔEFG with ∠ FGH as its exterior angle
ext. ∠FGH = ∠F + ∠E
125° = 55° + x
x = 125° - 55°
x = 70°
Thus, x = 70° and y = 55°
APPEARS IN
संबंधित प्रश्न
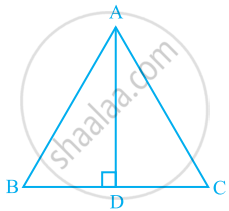
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
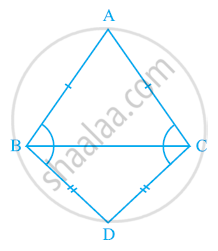
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
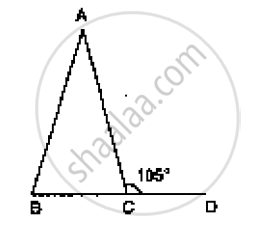
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
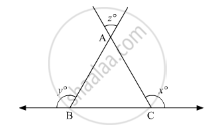
In the given figure, what is z in terms of x and y?
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
