Advertisements
Advertisements
प्रश्न
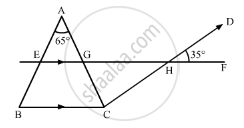
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
उत्तर
In the given figure,,AB || CD,EF || BC ∠BAC = 65° and ∠DHF = 35°
We need to find ∠AGH
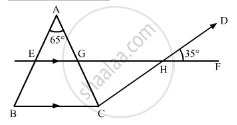
Here, GF and CD are straight lines intersecting at point H, so using the property, “vertically opposite angles are equal”, we get,
∠DHF = ∠GHC
∠GHC = 35°
Further, as AB || CD and AC is the transversal
Using the property, “alternate interior angles are equal”
∠BAC = ∠ACD
∠ACD = 65°
Further applying angle sum property of the triangle
In ΔGHC
∠GHC + ∠HCG + CGH = 180°
∠CGH + 35° + 65° = 180°
100 + ∠CGH = 180°
∠CGH = 180°- 100°
∠CGH = 80°
Hence, applying the property, “angles forming a linear pair are supplementary”
As AGC is a straight line
∠CGH + ∠AGH = 180°
∠AGH + 80° = 180°
∠AGH + 180° - 80°
∠AGH = 100°
Therefore, ∠AGH = 100°
APPEARS IN
संबंधित प्रश्न
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
Can a triangle have two acute angles?Justify your answer in case.
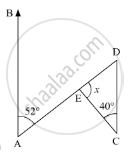
Compute the value of x in the following figure:
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
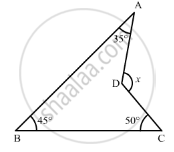
In the given figure, compute the value of x.
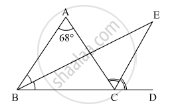
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
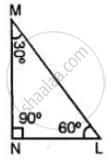
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Classify the following triangle according to angle:
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
The number of triangles in figure is ______.