Advertisements
Advertisements
Question
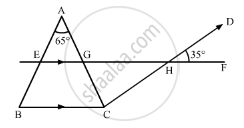
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
Solution
In the given figure,,AB || CD,EF || BC ∠BAC = 65° and ∠DHF = 35°
We need to find ∠AGH
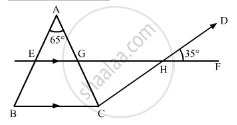
Here, GF and CD are straight lines intersecting at point H, so using the property, “vertically opposite angles are equal”, we get,
∠DHF = ∠GHC
∠GHC = 35°
Further, as AB || CD and AC is the transversal
Using the property, “alternate interior angles are equal”
∠BAC = ∠ACD
∠ACD = 65°
Further applying angle sum property of the triangle
In ΔGHC
∠GHC + ∠HCG + CGH = 180°
∠CGH + 35° + 65° = 180°
100 + ∠CGH = 180°
∠CGH = 180°- 100°
∠CGH = 80°
Hence, applying the property, “angles forming a linear pair are supplementary”
As AGC is a straight line
∠CGH + ∠AGH = 180°
∠AGH + 80° = 180°
∠AGH + 180° - 80°
∠AGH = 100°
Therefore, ∠AGH = 100°
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if ∠A = 55°, ∠B = 40°, find ∠C.
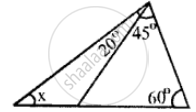
In the following, find the marked unknown angle:

In the following, find the marked unknown angle:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
15 cm, 20 cm, 25 cm
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
Which two triangles have ∠B in common?