Advertisements
Advertisements
Question
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
Solution
In the given problem, the sum of two angles of a triangle is equal to its third angle.
We need to find the measure of the third angle.
Thus, it is given, in ΔABC
A+B+C ........(1)
Now, according to the angle sum property of the triangle, we get,
∠A +∠B + ∠C = 180°
∠C + ∠C = 180° (Using 1)
2∠C = 180°
`∠C = (180°)/2`
∠C = 90°
Therefore, the measure of the third angle is
∠C = 90°.
APPEARS IN
RELATED QUESTIONS
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
OR
ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
In the given figure, AB || DE. Find ∠ACD.

Fill in the blank to make the following statement true:
An exterior angle of a triangle is equal to the two ....... opposite angles.
Mark the correct alternative in each of the following:
If all the three angles of a triangle are equal, then each one of them is equal to
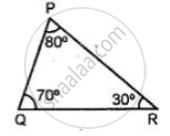
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
Classify the following triangle according to angle:
In the given figure, AB is parallel to CD. Then the value of b is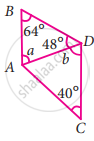
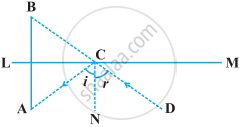
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
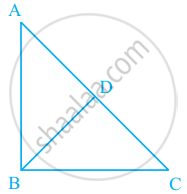
In figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is ______.