Advertisements
Advertisements
Question
In the given figure, AB || DE. Find ∠ACD.

Solution
In the given problem, AB || DE
We need to find ∠ACD
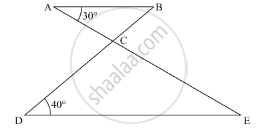
Now, AB || DE and AEis the transversal, so using the property, “alternate interior angles are equal”, we get,
∠BAE = ∠AED
∠AED = 30
Further, applying angle sum property of the triangle
In ΔDCE
∠DCE + ∠D + ∠E = 180
∠DCE + 40 + 30 = 180
∠DCE + 70 = 180
∠DCE = 180° - 70°
∠DCE = 110°
Further, ACE is a straight line, so using the property, “the angles forming a linear pair are supplementary”, we get,
∠ACD + ∠DCE = 180°
∠ACD + 110 = 180°
∠ACD = 180 - 110°
∠ACD = 70°
Therefore, ∠ACD = 70° .
APPEARS IN
RELATED QUESTIONS
ABC is a triangle in which ∠A — 72°, the internal bisectors of angles B and C meet in O.
Find the magnitude of ∠BOC.
Is the following statement true and false :
All the angles of a triangle can be greater than 60°.
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
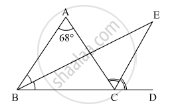
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
Calculate the unknown marked angles of the following figure :
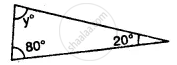
Find x, if the angles of a triangle is:
x°, 2x°, 2x°
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
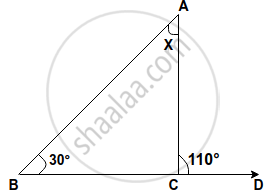
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
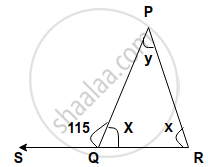
Find, giving a reason, the unknown marked angles, in a triangle drawn below:

