Advertisements
Advertisements
Question
ABC is a triangle in which ∠A — 72°, the internal bisectors of angles B and C meet in O.
Find the magnitude of ∠BOC.
Solution
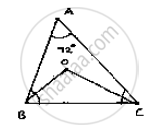
Given,
ABC is a triangle
`∠ A=72^@` and internal bisector of angles B and C meeting O
In` Δ ABC = ∠ A+∠ B+∠ C=180^@`
⇒`72^@+∠ B+∠ C=180^@`
⇒`∠ B+∠C =180^@-72^@ ` divide both sides by ‘2’
⇒`∠ B/2+∠ C/2=108^@/2` ..................(1)
⇒`∠ OBC +∠ OCB =54^@` ...................(1)
Now in `Δ BOC⇒ ∠OBC +∠ OCB +∠ BOC = 180^@`
⇒ `54^@+∠BOC=180^@`
⇒ `∠BOC=180^@-54^@=126^@`
∴` ∠ BOC=126^@`
APPEARS IN
RELATED QUESTIONS
Can a triangle have two acute angles?Justify your answer in case.
Can a triangle have All angles more than 60°? Justify your answer in case.
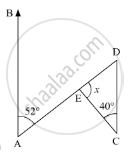
Compute the value of x in the following figure:
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
If the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
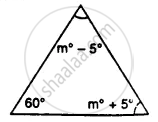
Find the unknown marked angles in the given figure:
Classify the following triangle according to sides:
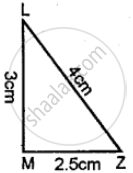
Classify the following triangle according to sides:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
17 cm, 7 cm, 8 cm
