Advertisements
Advertisements
Question
The angles of a triangle are arranged in ascending order of magnitude. If the difference
between two consecutive angles is 10°, find the three angles.
Solution
Given that,
The difference between two consecutive angles is `10^@`
Let x,x+10,x+20 be the consecutive angles differ by `10^@`
W.K.T sum of all angles of traingle is `180^@`
`x+x+10+x+20=180^@`
`3x+30=180^@`
⇒ `3x=180-30^@ ⇒ 3x=150^@`
⇒`x=50^@`
∴ `x=50^@`
∴ The required angles are
x,x+10 and x+20
x=50
x+10=50+10=60
x+20=50+10+10=70
The difference between two consecutive angles is `10^@` then three angles are ` 50^@,60^@ and 70^@`
APPEARS IN
RELATED QUESTIONS
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
OR
ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
In ΔABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
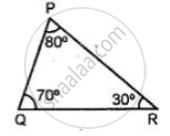
Find the unknown marked angles in the given figure:
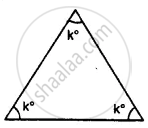
Classify the following triangle according to angle:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
12 cm, 12 cm, 16 cm
Can you draw a triangle with 25°, 65° and 80° as angles?
In ΔABC, name the 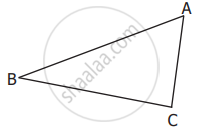
a) Three sides: _________, __________, __________
b) Three Angles: _________, __________, __________
c) Three Vertices: _________, __________, __________
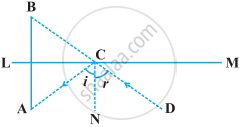
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
Can we have two acute angles whose sum is an acute angle? Why or why not?
