Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Definition
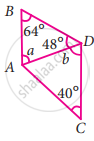
Triangle: A triangle is a closed figure made by joining three non-collinear points by line segments. A triangle is a three-sided polygon.
Notes
Triangles:
-
A triangle is a three-sided polygon. In fact, it is the polygon with the least number of sides.
- A triangle is a closed figure made by joining three non-collinear points by line segments.
-
It has three sides, three angles, and three vertices.
- The vertices, sides and angles of a triangle are called the parts of the triangle.
- We write ∆ABC instead of writing "Triangle ABC".
- ‘Length of line segment AB’ is written as l(AB).
- The three sides of the triangle are `bar"AB", bar"BC", and bar"CA"`.
The three angles are ∠BAC, ∠BCA, and ∠ABC.
The points A, B, and C are called the vertices of the triangle.
-
Being a polygon, a triangle has an exterior and an interior.
- P is in the interior of the triangle, R is in the exterior and Q on the triangle.
If you would like to contribute notes or other learning material, please submit them using the button below.
Shaalaa.com | Triangle
to track your progress