Advertisements
Advertisements
Question
In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
Solution
In the given ΔABC, BD⊥AC and CE⊥AB.
We need prove ∠BOC = 180° - ∠A
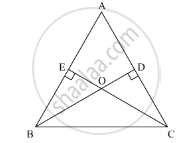
Here, in ΔBDC, using the exterior angle theorem, we get,
∠BDA = ∠DBC + ∠DBC
90 = ∠DBO + ∠DBC ................ (1)
Similarly, in ΔEBC, we get,
∠AEC = ∠EBC + ∠ECB
90 = ∠EBC ∠ECB ................ (2)
Adding (1) and (2), we get,
90 + 90 = ∠DBC + ∠DCB + ∠EBC + ∠ECB
180 = (∠DCB +∠EBC) + (∠DBC+∠ECB)................ (3)
Now, on using angle sum property,
In ΔABC, we get,
∠BAC + ∠ABC + ∠ACB = 180
∠ABC + ∠ACB = 180 - ∠BAC
This can be written as,
∠EBC + ∠DCB = 180 - ∠A ......... (4)
Similarly, using angle sum property in ΔOBC, we get,
∠BOC + ∠OBC + ∠OCB = 180
∠OBC + ∠OCB = 180 - ∠BOC
This can be written as,
∠DBC + ∠ECB = 180 - ∠BOC ......... (5)
Now, using the values of (4) and (5) in (3), we get,
180 = 180 - ∠BOC ........... (5)
180 = 360 - ∠A - ∠BOC
∠BOC = 360 - 180 - ∠A
∠BOC = 180 - ∠A
Therefore, ∠BOC = 180 - ∠A.
Hence proved
APPEARS IN
RELATED QUESTIONS
In the given figure, AB || DE. Find ∠ACD.

Is the following statement true and false :
All the angles of a triangle can be less than 60°
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
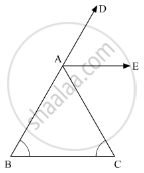
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
In ΔABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
In the following, find the marked unknown angle:

The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
The correct statement out of the following is 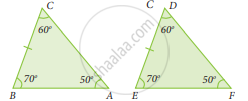
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
