Advertisements
Advertisements
Question
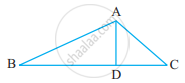
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
Solution
In the given ΔABC, AD bisects ∠Aand ∠C >∠B. We need to prove ∠ADB >∠ADC.
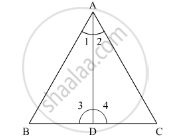
Let,
∠BAD = ∠1
∠DAC = ∠2
∠ADB = ∠3
∠ADC = ∠4
Also,
As AD bisects ∠A,
∠1 = ∠2…..(1)
Now, in ΔABD, using exterior angle theorem, we get,
∠4 = ∠B + ∠1
Similarly,
∠3 = ∠2 + ∠C
∠3 = ∠1 + ∠C [using (1)]
Further, it is given,
∠C >∠B
Adding ∠1to both the sides
∠C +∠1 >∠B + ∠1
∠3 > ∠4
Thus, ∠3 > ∠4
Hence proved.
APPEARS IN
RELATED QUESTIONS
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

Is the following statement true and false :
All the angles of a triangle can be less than 60°
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Classify the following triangle according to sides:
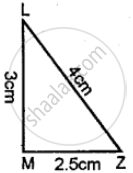
The length of the sides of the triangle is given. Say what types of triangles they are 3 cm, 4 cm, 5 cm.
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
In figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is ______.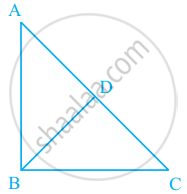
The number of triangles in figure is ______. Their names are ______.
What is common in the following figure?
 |
 |
| (i) | (ii) |
Is figure (i) that of triangle? if not, why?
Which two triangles have ∠B in common?