Advertisements
Advertisements
प्रश्न
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
उत्तर
In the given ΔABC, AD bisects ∠Aand ∠C >∠B. We need to prove ∠ADB >∠ADC.
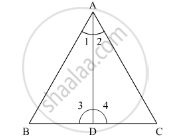
Let,
∠BAD = ∠1
∠DAC = ∠2
∠ADB = ∠3
∠ADC = ∠4
Also,
As AD bisects ∠A,
∠1 = ∠2…..(1)
Now, in ΔABD, using exterior angle theorem, we get,
∠4 = ∠B + ∠1
Similarly,
∠3 = ∠2 + ∠C
∠3 = ∠1 + ∠C [using (1)]
Further, it is given,
∠C >∠B
Adding ∠1to both the sides
∠C +∠1 >∠B + ∠1
∠3 > ∠4
Thus, ∠3 > ∠4
Hence proved.
APPEARS IN
संबंधित प्रश्न
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
Can a triangle have All angles more than 60°? Justify your answer in case.
In the given figure, AB || DE. Find ∠ACD.

In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
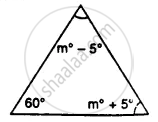
Find the unknown marked angles in the given figure:
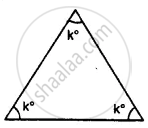
Find the unknown marked angles in the given figure:
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
Can 30°, 60° and 90° be the angles of a triangle?
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
The number of triangles in figure is ______.