Advertisements
Advertisements
प्रश्न
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
उत्तर
Given that,
Two angles are equal and the third angle is greater than each of those angles `by 30^@` Let x, x, x+30 be the angles of a triangle
We know that
Sum of all angles of a triangle is `180^@`
`x+x+x+30=180^@`
`3x+30=180^@`
`3x=180^@-30^@`
`3x=150^@`
`x=150^@/3`
`x=50^@`
∴ The angles are x,x,x+30
`x=50^@`
`x+30=80^@`
∴ The required angles are `50^@,50^@, 80^@`
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
All the angles of a triangle can be less than 60°
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
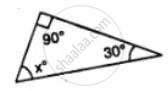
Find the value of the angle in the given figure:

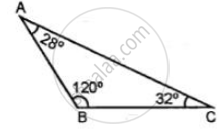
Find the unknown marked angles in the given figure:
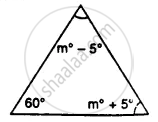
Calculate the unknown marked angles of the following figure :
Classify the following triangle according to angle:
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
