Advertisements
Advertisements
प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
उत्तर
Given that
The angles of triangle are
`(x-40^@),(x-20)^@ and (x/2-10)^@`
We know that
Sum of all angles of traingle is `180^@`
∴ `x-40^@+x-20^@+x/2-10^@=180^@`
`2x+x/2-70^@=180^@`
`(5x)/2=180+70^@`
`5x=250^@(2)`
`x=50^@(2)`
`x=100^@`
∴ `x=100^@`
APPEARS IN
संबंधित प्रश्न
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
ABC is a triangle in which ∠A — 72°, the internal bisectors of angles B and C meet in O.
Find the magnitude of ∠BOC.
In the given figure, AB || DE. Find ∠ACD.

An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
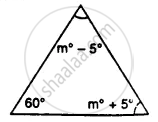
Find the value of the angle in the given figure:

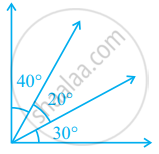
Find the unknown marked angles in the given figure:
One angle of a right-angled triangle is 70°. Find the other acute angle.
Classify the following triangle according to sides:
The number of angles in figure is ______.