Advertisements
Advertisements
प्रश्न
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
उत्तर
Given that the angles of a triangle are in the ratio 1: 2 : 3
Let the angles be a, 2a,3a
∴ We know that
Sum of all angles of triangles is `180^@`
`a+2a+3a=180^@`
`6a=180^@`
`a=180^@/6`
`a=30^@`
Since` a=30^@`
`2a=2(30)^@=60^@`
`3a=3(30)^@=90^@`
∴ angles are a =` 30^@,2a=60^@,3a=90^@`
∴ Hence angles are `30^@,60^@ and 90^@`
APPEARS IN
संबंधित प्रश्न
If two acute angles of a right triangle are equal, then each acute is equal to
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
Find the unknown marked angles in the given figure:
One angle of a right-angled triangle is 70°. Find the other acute angle.
Find, giving a reason, the unknown marked angles, in a triangle drawn below:

The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
12 cm, 12 cm, 16 cm
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.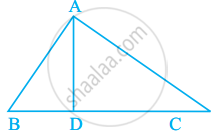
Identify three triangles in the figure.