Advertisements
Advertisements
प्रश्न
If two acute angles of a right triangle are equal, then each acute is equal to
विकल्प
30°
45°
60°
90°
उत्तर
In the given problem, we have a right angled triangle and the other two angles are equal.
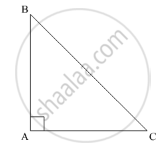
So, In ΔABC
∠A = 90°
∠B = ∠C
Now, using the angle sum property of the triangle, in ΔABC, we get,
∠A + ∠B + ∠C = 180°
90° + 2∠B = 180° (∠B = ∠C)
2∠B= 180° - 90°
`∠B = (90°)/2`
∠B = 45°
APPEARS IN
संबंधित प्रश्न
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
In the given figure, AB || DE. Find ∠ACD.

In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
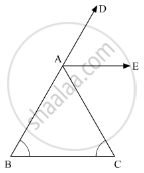
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
Find the unknown marked angles in the given figure:
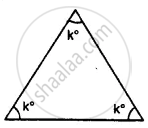
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
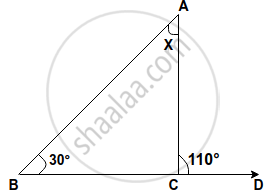
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
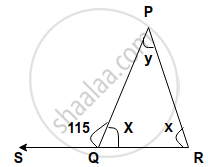
The angles of a triangle are in the ratio 2 : 3 : 4. Then the angles are
In a ∆ABC, AB = AC. The value of x is ________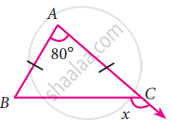
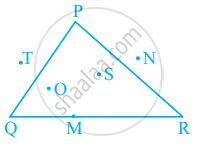
In figure, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.