Advertisements
Advertisements
प्रश्न
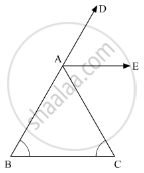
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
उत्तर
In the given problem, AE bisects ∠CAD and ∠B = ∠C
We need to prove AE || BC
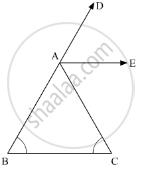
As, ∠CAD is bisected by AE
∠CAD = 2∠CAE - 2∠DAE ..........(1)
Now, using the property, “an exterior angle of a triangle in equal to the sum of the two opposite interior angles”, we get,
∠CAD ∠B +∠C
∠CAD = 2∠C (∠B = ∠C)
2∠CAE = 2∠C (using 1)
∠CAE = ∠C
∠CAE = ∠ACB
Hence, using the property, if alternate interior angles are equal, then the two lines are parallel, we get,
∠CAE = ∠ACB
Thus,AE || BC
Hence proved.
APPEARS IN
संबंधित प्रश्न
If the bisectors of the base angles of a triangle enclose an angle of 135°, prove that the triangle is a right triangle.
Is the following statement true and false :
All the angles of a triangle can be equal to 60°.
If the angles of a triangle are equal, find its angles.
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Find the unknown marked angles in the given figure:

Classify the following triangle according to sides:
Find all the three angles of the ΔABC
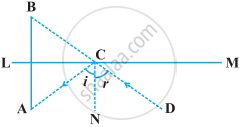
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
The number of angles in figure is ______.