Advertisements
Advertisements
Question
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
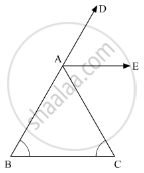
Solution
In the given problem, AE bisects ∠CAD and ∠B = ∠C
We need to prove AE || BC
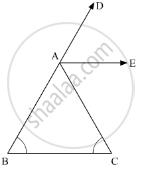
As, ∠CAD is bisected by AE
∠CAD = 2∠CAE - 2∠DAE ..........(1)
Now, using the property, “an exterior angle of a triangle in equal to the sum of the two opposite interior angles”, we get,
∠CAD ∠B +∠C
∠CAD = 2∠C (∠B = ∠C)
2∠CAE = 2∠C (using 1)
∠CAE = ∠C
∠CAE = ∠ACB
Hence, using the property, if alternate interior angles are equal, then the two lines are parallel, we get,
∠CAE = ∠ACB
Thus,AE || BC
Hence proved.
APPEARS IN
RELATED QUESTIONS
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
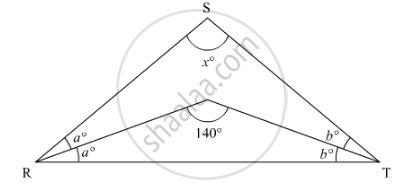
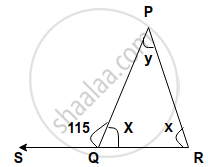
In ΔRST (See figure), what is the value of x?
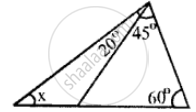
In the following, find the marked unknown angle:
Can a triangle together have the following angles?
85°, 95° and 22°
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
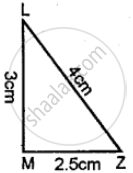
Classify the following triangle according to sides:
The correct statement out of the following is 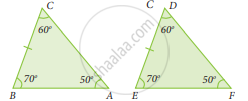
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
