Advertisements
Advertisements
Question
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
Options
55°
85°
40°
9.0°
Solution
In the given ΔABC, ∠DAC = 95° and ∠A = 55°

Now, according to the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”, we get,
∠A + ∠B = ∠ACD
55° + ∠B = 95°
∠B = 95° - 55°
= 40°
So, ∠B = 40°
APPEARS IN
RELATED QUESTIONS
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
Can a triangle have two obtuse angles? Justify your answer in case.
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
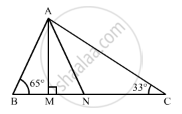
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
In ΔPQR, If ∠R > ∠Q then ______.
Find the unknown marked angles in the given figure:

In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
The correct statement out of the following is