Advertisements
Advertisements
Question
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
Solution
∠A + ∠B + ∠C= 180°
⇒ 62° + 62° + ∠C = 180°
⇒ 124° + ∠C = 180°
⇒ ∠C = 180° – 124°
⇒∠C = 56°
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if ∠A = 55°, ∠B = 40°, find ∠C.
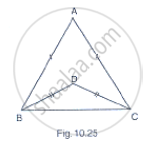
In Fig. 10.25, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD.
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
OR
ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Is the following statement true and false :
A triangle can have two obtuse angles.
Fill in the blank to make the following statement true:
An exterior angle of a triangle is equal to the two ....... opposite angles.
Fill in the blank to make the following statement true:
A triangles cannot have more than ......obtuse angles.
Can a triangle together have the following angles?
85°, 95° and 22°
Can 30°, 60° and 90° be the angles of a triangle?
In the given figure, AB is parallel to CD. Then the value of b is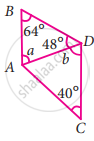
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
