Advertisements
Advertisements
Question
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
Solution
∠A + ∠B + ∠C = 180°
⇒ 100° + ∠B + ∠B = 180°
⇒ 2∠B = 180° 100°
∠B = `(80°)/2`
∠B = 40°
∠C = ∠B = 40°
APPEARS IN
RELATED QUESTIONS
Compute the value of x in the following figure:
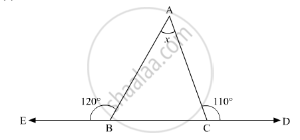
Compute the value of x in the following figure:
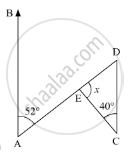
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
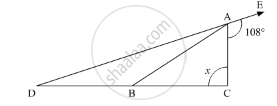
One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
Can a triangle together have the following angles?
33°, 74° and 73°
Can a triangle together have the following angles?
85°, 95° and 22°
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
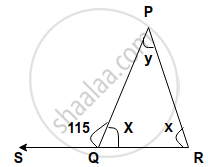
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.