Advertisements
Advertisements
Question
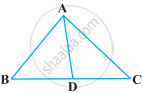
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.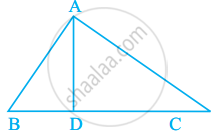
Options
1
2
3
4
Solution
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is 3.
Explanation:
A triangle, in which one angle is equal to 90° is called a right-angled triangle.
Since, ∠BAC = 90°
ΔBAC is a right-angled triangle.
Also, ∠ADB = ∠ADC = 90° ......[ AD Perpendicular to BC]
∠ADB and ∠ADC are also right-angled triangles.
Hence, there are 3 right-angled triangles.
APPEARS IN
RELATED QUESTIONS
Can a triangle have All angles equal to 60°? Justify your answer in case.
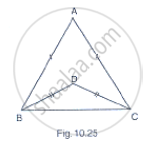
In Fig. 10.25, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD.
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
Mark the correct alternative in each of the following:
If all the three angles of a triangle are equal, then each one of them is equal to
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
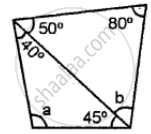
In the following, find the marked unknown angle:
In a ∆ABC, AB = AC. The value of x is ________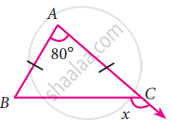
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.
Can we have two acute angles whose sum is a reflex angle? Why or why not?
