Advertisements
Advertisements
Question
In figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆PQR is ______.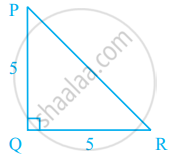
Options
A right triangle but not isosceles
An isosceles right triangle
Isosceles but not a right triangle
Neither isosceles nor right triangle
Solution
In figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆PQR is an isosceles right triangle.
Explanation:
Since, PQ Perpendicular to RQ
So, ∆PQR = 90°
∴ ∆PQR is right-angled triangle.
Also, in ΔPQR,
PQ = QR
ΔPQR is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
Can a triangle together have the following angles?
85°, 95° and 22°
Find x, if the angles of a triangle is:
x°, x°, x°
Classify the following triangle according to sides:
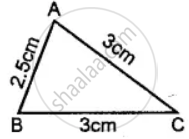
The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
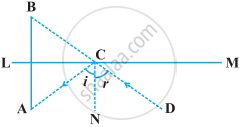
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
Can we have two acute angles whose sum is a straight angle? Why or why not?
