Advertisements
Advertisements
Question
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
Options
40°
35°
50°
45°
Solution
35°
Explanation;
Hint:
3x – 40 + x + 20 + 2x – 10 = 180° ...(Sum of the angles of a triangle is 180°)
6x – 30 = 180°
6x = 180° + 30°
x = `(210^circ)/(6^circ)`
= 35°
APPEARS IN
RELATED QUESTIONS
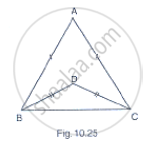
In Fig. 10.25, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

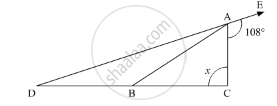
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
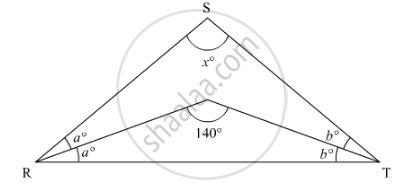
In ΔRST (See figure), what is the value of x?
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
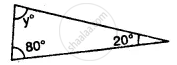
Calculate the unknown marked angles of the following figure :
In the given figure, show that: ∠a = ∠b + ∠c
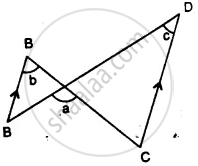
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
In the following, find the marked unknown angle:
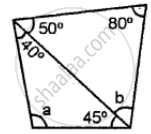
Can 30°, 60° and 90° be the angles of a triangle?
Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is point A in its exterior or in its interior?
