Advertisements
Advertisements
Question
In the following, find the marked unknown angle:
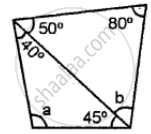
Solution
Since, sum of all angles of triangle = 180°
1st Triangle 50° + 80° + b = 180°
⇒ 130°+ &= 180°
⇒ b = 180° – 130°
b = 50°
II nd Triangle 40° + 45° + a = 180°
⇒ 85° + a = 180°
⇒ a = 180° - 85
a = 95°
APPEARS IN
RELATED QUESTIONS
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
ABC is a triangle in which ∠A — 72°, the internal bisectors of angles B and C meet in O.
Find the magnitude of ∠BOC.
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Can a triangle have two right angles? Justify your answer in case.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
Is the following statement true and false :
All the angles of a triangle can be less than 60°
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
Find x, if the angles of a triangle is:
x°, 2x°, 2x°
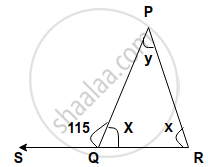
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
Can 30°, 60° and 90° be the angles of a triangle?
