Advertisements
Advertisements
Question
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
Solution
Given that
The angles of triangle are
`(x-40^@),(x-20)^@ and (x/2-10)^@`
We know that
Sum of all angles of traingle is `180^@`
∴ `x-40^@+x-20^@+x/2-10^@=180^@`
`2x+x/2-70^@=180^@`
`(5x)/2=180+70^@`
`5x=250^@(2)`
`x=50^@(2)`
`x=100^@`
∴ `x=100^@`
APPEARS IN
RELATED QUESTIONS
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
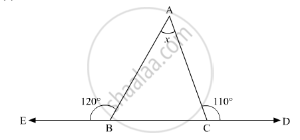
Compute the value of x in the following figure:
Is the following statement true and false :
All the angles of a triangle can be greater than 60°.
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
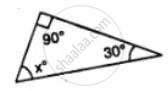
Calculate the unknown marked angles of the following figure :
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
Can a triangle together have the following angles?
33°, 74° and 73°
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
12 cm, 12 cm, 16 cm
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
