Advertisements
Advertisements
Question
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
Solution
In Δ ABC,

∵ AB = AC.
∴ ∠B = ∠C
But ∠A = 100°
and ∠A + ∠B + ∠C = 180° ..........(Angles of a triangle)
⇒ 100° + ∠B + ∠B = 180°
⇒ 2 ∠B = 180°− 100°
⇒ 2 ∠B = 80°
∴ ∠B =`(80°)/2=40°`
Hence ∠B = ∠C = 40°
APPEARS IN
RELATED QUESTIONS
Fill in the blank to make the following statement true:
An exterior angle of a triangle is equal to the two ....... opposite angles.
Define a triangle.
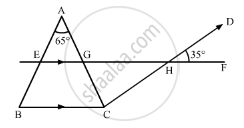
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
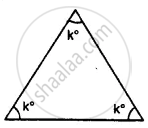
Find the unknown marked angles in the given figure:
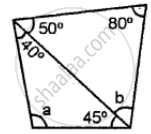
One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
In the following, find the marked unknown angle:
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
Classify the following triangle according to sides:
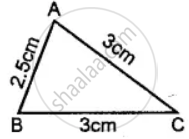
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
8.4 cm, 16.4 cm, 4.9 cm
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
