Advertisements
Chapters
2: Rational Numbers
3: Fractions (Including Problems)
4: Decimal Fractions (Decimals)
5: Exponents (Including Laws of Exponents)
6: Ratio and Proportion (Including Sharing in a Ratio)
7: Unitary Method (Including Time and Work)
8: Percent and Percentage
9: Profit, Loss and Discount
10: Simple Interest
11: Fundamental Concepts (Including Fundamental Operations)
12: Simple Linear Equations (Including Word Problems)
13: Set Concepts (Some Simple Divisions by Vedic Method)
14: Lines and Angles (Including Construction of angles)
▶ 15: Triangles
16: Pythagoras Theorem
17: Symmetry (Including Reflection and Rotation)
18: Recognition of Solids (Representing 3-D in 2-D)
19: Congruency: Congruent Triangles
20: Mensuration
21: Data Handling
22: Probability
![Selina solutions for Concise Mathematics [English] Class 7 ICSE chapter 15 - Triangles - Shaalaa.com](/images/concise-mathematics-english-class-7-icse_6:880cdcd6265b4864b6486afbf92875b0.jpg "Selina solutions for Concise Mathematics [English] Class 7 ICSE chapter 15 - Triangles")
Advertisements
Solutions for Chapter 15: Triangles
Below listed, you can find solutions for Chapter 15 of CISCE Selina for Concise Mathematics [English] Class 7 ICSE.
Selina solutions for Concise Mathematics [English] Class 7 ICSE 15 Triangles Exercise 15 (A)
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
If the angles of a triangle are equal, find its angles.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Calculate the unknown marked angles of the following figure :
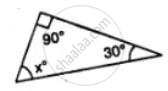
Calculate the unknown marked angles of the following figure :
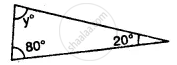
Calculate the unknown marked angles of the following figure :
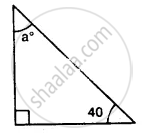
Find the value of the angle in the given figure:
Find the value of the angle in the given figure:
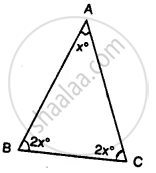
Find the unknown marked angles in the given figure:
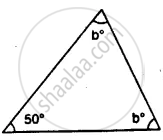
Find the unknown marked angles in the given figure:
Find the unknown marked angles in the given figure:
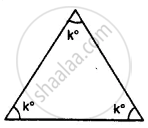
Find the unknown marked angles in the given figure:
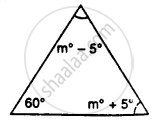
In the given figure, show that: ∠a = ∠b + ∠c
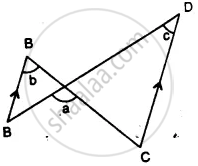
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
Find the unknown marked angles in the given figure:
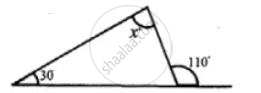
Find the unknown marked angles in the given figure:
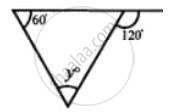
Find the unknown marked angles in the given figure:
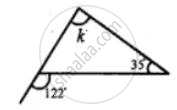
Find the unknown marked angles in the given figure:
Find the unknown marked angles in the given figure:
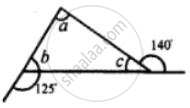
Find the unknown marked angles in the given figure:
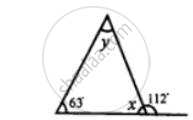
Find the unknown marked angles in the given figure:
Find the unknown marked angles in the given figure:
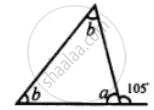
Find the unknown marked angles in the given figure:
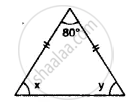
Selina solutions for Concise Mathematics [English] Class 7 ICSE 15 Triangles Exercise 15 (B)
Find the unknown angles in the given figure:
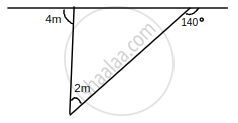
Find the unknown angles in the given figure:
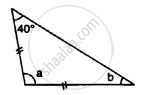
Find the unknown angles in the given figure:
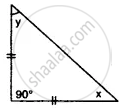
Find the unknown angles in the given figure:
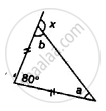
Find the unknown angles in the given figure:
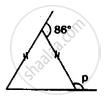
Find the unknown angles in the given figure:
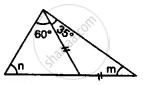
Find the unknown angles in the given figure:
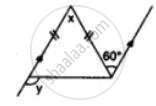
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
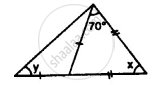
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
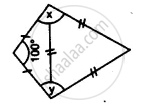
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
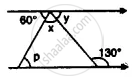
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
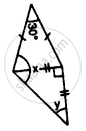
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
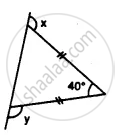
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
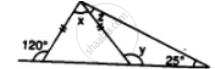
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
One of the base angles of an isosceles triangle is 52°. Find its angle of the vertex.
In an isosceles triangle, each base angle is four times its vertical angle. Find all the angles of the triangle.
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
The vertical angle of an isosceles triangle is three times the sum of its base angles. Find each angle.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1: 4. Find each angle of the triangle.
In the given figure, BI is the bisector of ∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.
In the given figure, express a in terms of b.
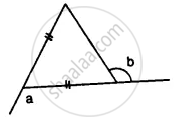
In Figure, BP bisects ∠ABC and AB = AC. Find x.
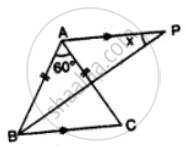
Find x in Figure Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.
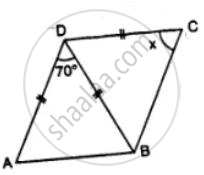
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠ABE
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠BAE
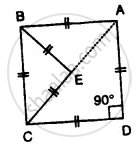
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.
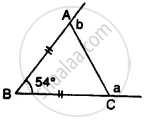
Selina solutions for Concise Mathematics [English] Class 7 ICSE 15 Triangles Exercise 15 (C)
Construct a ∆ABC such that:
AB = 6 cm, BC = 4 cm and CA = 5.5 cm
Construct a ∆ABC such that:
CB = 6.5 cm, CA = 4.2 cm and BA = 51 cm
Construct a ∆ABC such that:
BC = 4 cm, AC = 5 cm and AB = 3.5 cm
Construct a ∆ ABC such that:
AB = 7 cm, BC = 5 cm and ∠ABC = 60°
Construct a ∆ ABC such that:
BC = 6 cm, AC = 5.7 cm and ∠ACB = 75°
Construct a ∆ ABC such that:
AB = 6.5 cm, AC = 5.8 cm and ∠A = 45°
Construct a ∆ PQR such that :
PQ = 6 cm, ∠Q = 60° and ∠P = 45°. Measure ∠R.
Construct a ∆ PQR such that:
QR = 4.4 cm, ∠R = 30° and ∠Q = 75°. Measure PQ and PR.
Construct a ∆ PQR such that:
PR = 5.8 cm, ∠P = 60° and ∠R = 45°. Measure ∠Q and verify it by calculations
Construct an isosceles Δ ABC such that:
Base BC = 4 cm and base angle = 30°. Measure the other two sides of the triangle.
Construct an isosceles Δ ABC such that:
Base AB = 6.2 cm and base angle = 45°. Measure the other two sides of the triangle.
Construct an isosceles Δ ABC such that:
Base AC = 5 cm and base angle = 75°. Measure the other two sides of the triangle.
Construct an isosceles ∆ ABC such that:
AB = AC = 6.5 cm and ∠A = 60°
Construct an isosceles ∆ ABC such that:
One of the equal sides = 6 cm and vertex angle = 45°. Measure the base angles.
Construct an isosceles ∆ ABC such that:
BC = AB = 5.8 cm and ZB = 30°. Measure ∠A and ∠C.
Construct an equilateral Δ ABC such that:
AB = 5 cm. Draw the perpendicular bisectors of BC and AC. Let P be the point of intersection of these two bisectors. Measure PA, PB, and PC.
Construct an equilateral Δ ABC such that:
Each side is 6 cm.
Construct a ∆ ABC such that AB = 6 cm, BC = 4.5 cm and AC = 5.5 cm. Construct a circumcircle of this triangle.
Construct an isosceles ∆ PQR such that PQ = PR = 6.5 cm and ∠PQR = 75°. Using a ruler and compasses only constructs a circumcircle to this triangle.
Construct an equilateral triangle ABC such that it's one side = 5.5 cm. Construct a circumcircle to this triangle.
Construct a ∆ ABC such that AB = 6 cm, BC = 5.6 cm and CA = 6.5 cm. Inscribe a circle to this triangle and measure its radius.
Construct an isosceles ∆ MNP such that base MN = 5.8 cm, base angle MNP = 30°. Construct an incircle to this triangle and measure its radius.
Construct an equilateral ∆ DEF whose one side is 5.5 cm. Construct an incircle to this triangle.
Construct a ∆ PQR such that PQ = 6 cm, ∠QPR = 45° and angle PQR = 60°. Locate its incentre and then draw its incircle.
Solutions for 15: Triangles
Selina solutions for Concise Mathematics [English] Class 7 ICSE chapter 15 - Triangles
Shaalaa.com has the CISCE Mathematics Concise Mathematics [English] Class 7 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Concise Mathematics [English] Class 7 ICSE CISCE 15 (Triangles) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concise Mathematics [English] Class 7 ICSE chapter 15 Triangles are Concept for Angle Sum Property, Concept for Exterior Angle Property, Concept for Construction of Simple Triangles., Concept of Triangles.
Using Selina Concise Mathematics [English] Class 7 ICSE solutions Triangles exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Concise Mathematics [English] Class 7 ICSE students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 15, Triangles Concise Mathematics [English] Class 7 ICSE additional questions for Mathematics Concise Mathematics [English] Class 7 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
