Advertisements
Advertisements
Question
Construct a ∆ PQR such that:
PR = 5.8 cm, ∠P = 60° and ∠R = 45°. Measure ∠Q and verify it by calculations
Solution
Steps of Construction :
(i) Draw a line segment PR = 5.8 cm
(ii) At P, construct an angle of 60°
(iii) At R, draw another angle of 45° meeting each other at Q.
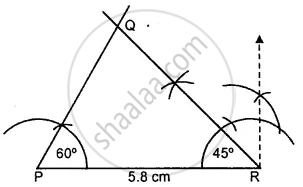
∆ PQR is the required triangle. On measuring ∠Q, it is 75°
Verification: We know that sum of angles of a triangle is 180°
∴∠P + ∠Q + ∠R = 180°
⇒ 60° + ∠Q + 45° = 180°
⇒ ∠Q + 105° = 180°
⇒ ∠Q = 180° – 105° = 75°.
APPEARS IN
RELATED QUESTIONS
Construct a ∆ ABC such that:
AB = 6.5 cm, AC = 5.8 cm and ∠A = 45°
Construct a ∆ PQR such that:
QR = 4.4 cm, ∠R = 30° and ∠Q = 75°. Measure PQ and PR.
Construct an isosceles Δ ABC such that:
Base BC = 4 cm and base angle = 30°. Measure the other two sides of the triangle.
Construct an isosceles ∆ ABC such that:
AB = AC = 6.5 cm and ∠A = 60°
Construct an isosceles ∆ ABC such that:
BC = AB = 5.8 cm and ZB = 30°. Measure ∠A and ∠C.
Construct an equilateral Δ ABC such that:
AB = 5 cm. Draw the perpendicular bisectors of BC and AC. Let P be the point of intersection of these two bisectors. Measure PA, PB, and PC.
Construct an isosceles ∆ PQR such that PQ = PR = 6.5 cm and ∠PQR = 75°. Using a ruler and compasses only constructs a circumcircle to this triangle.
Construct a ∆ ABC such that AB = 6 cm, BC = 5.6 cm and CA = 6.5 cm. Inscribe a circle to this triangle and measure its radius.
Construct an isosceles ∆ MNP such that base MN = 5.8 cm, base angle MNP = 30°. Construct an incircle to this triangle and measure its radius.
Construct a ∆ PQR such that PQ = 6 cm, ∠QPR = 45° and angle PQR = 60°. Locate its incentre and then draw its incircle.
