Advertisements
Advertisements
Question
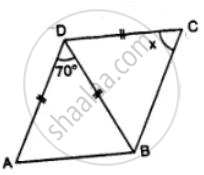
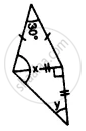
Find x in Figure Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.
Solution
In the figure,
DA = DB = DC
BD bisects ∠ABC
and ∠ADB = 70°

But ∠ADB + ∠DAB + ∠DBA = 180° ............(Angles of a triangle)
⇒ 70° + ∠DBA + ∠DBA = 180° ........(∵ DA = DB)
⇒ 70° + 2 ∠DBA = 180°
⇒ 2 ∠DBA = 180° − 70°
= 110°
∴ ∠DBA =`(110°)/2=55°`
∵ BD is the bisector of ∠ABC,
∴ ∠DBA = ∠DBC = 55°
But in Δ DBC,
DB = DC
∴ ∠DCB = ∠DBC
⇒ x = 55°
APPEARS IN
RELATED QUESTIONS
Find the unknown angles in the given figure:
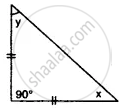
Find the unknown angles in the given figure:
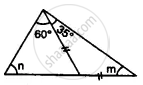
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
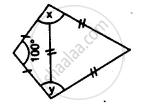
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
In an isosceles triangle, each base angle is four times its vertical angle. Find all the angles of the triangle.
The vertical angle of an isosceles triangle is three times the sum of its base angles. Find each angle.
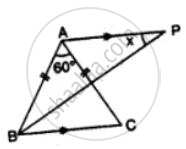
In Figure, BP bisects ∠ABC and AB = AC. Find x.
In the figure, AB is parallel to CD, find x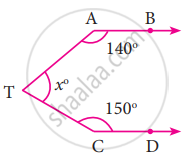
In the figure, AB is parallel to CD, find x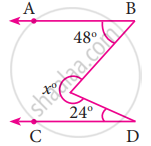
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle
